３．２． カオス符号の生成 　「カオス」とは決定論でありながらも長期予測が困難な振る舞いをいいます。 　この性質により、　暗号通信の分野での応用が期待されており、　ユーザ識別を行わせる拡散符号（つまり暗号でいう鍵の役割）への応用が考えられています。 　また非同期通信で良好な性質を示す負の自己相関特性を持つ符号は、　図４のカオス写像を用いることで、　簡単に、　しかも非常に多数の符号が設計できます[3]。 　このようなカオス符号を有限精度により実現した最大周期系列等も考えられています。

３．３． カオス符号から直交した符号の生成 　ある符号と互いに直交した符号の集合は、　下図の規則を適用すれば設計可能です。 　この方法を用いることで先ほど生成したカオス符号とそれと直交した符号が、　符号長２のｋ乗に対しｋ個生成されます。 　このようにして生成された直交カオス符号のもつ自己相関特性は、　元となったカオス符号と類似した特性を有していることが最近の研究で確かめられました[4]。 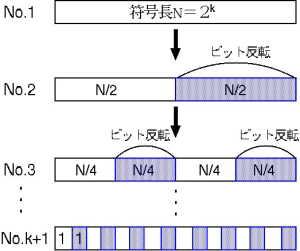図５．　直交符号の作り方