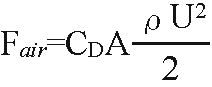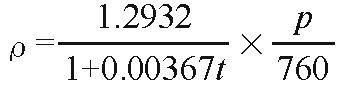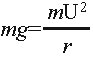|
技術的考察
ここいらで少し頭を使って、実現可能かどうかを検討してみましょう。
コストは無視です。無視(;。;)
○機体
リニアモーターカーに関しては、いろんなところで実用化に向けて着々と研究が進められています。
この「S計画」で使用するリニアモーターカーも基本的には現在のリニアモーターカーに関する技術を改善していくことで実現可能です。しかし、いくつか異なるところもでてくるので、その点に関して考察してみましょう。
まず、機体は真空中で使用されるため、完全な密閉型でなければなりません(生体が乗らない場合は密閉でなくてもよい)。また、密閉型であるため、機内の酸素量などを調整するために、酸素を積み込んでおくか、電気・化学的に合成できる装置を積み込んでおかなければなりません。要するにスペースシャトルを真空チューブ内に設置しリニアモーターで駆動するような感じです。技術的には何とかなりそうです。しかも、スペースシャトルと違って大気圏突入の必要がなく、障害物のない(空気もない)空間を移動するため、応力が生じないので、機体の強度はそれほど必要なく、推進用に大量の燃料を積み込む必要もありません。
次に、ふつうのリニアモーターカーは浮上させることだけ考えておけばよいですが、加速しすぎると遠心力で飛び出してしまうため、超高速走行時は機体の上部を磁力で押さえつけなければならない場合があります(下部から磁力で引っ張ることも考えられるが、低速時にしたから引っ張ると危険)。これも現在の技術で何とかなりそうです。
今回示した二つのモデルでは、実在するリニアモーターカーとほぼ同様のスペックを用いて、理論計算を行っています。機体自体は何とか作成できそうなので、示すチューブの条件が整えばこの「S計画」は実現可能になります。
○チューブの真空度
「S計画」ではこのチューブを如何に作るかがミソです。巨大なチューブを作るのにいくらかかるとか、どうやって海や山の中を通すのかはとりあえずおいといて、どの程度のスペックが要求されるのかを算出してみたいと思います。
リニアモーターカーは走行中に空気抵抗と加速抵抗を受けます。磁気浮上しているので転がり抵抗はありません。加速抵抗はあまり問題になりません。しかし、空気抵抗は高速になればなるほど加速的に大きくなっていきます。「S計画」のコンセプトはこの空気抵抗を減らそうということです。それでは実際に計算してみましょう。
リニアモーターカーが受ける力は
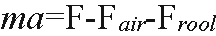
になります。
m:車体質量(kg)
a:加速度(kg)
F:推進力
Fair:空気抵抗
Frool:転がり抵抗
であり、磁気浮上していることからFrool:転がり抵抗は0になります。
最後の項は空気抵抗であり、
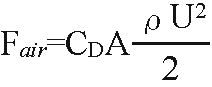
ここでCDは抗力係数で機体の形状で決まります。今回の計算でこの値は3とします。これは一般的な乗用車における値ですので、機体形状を流線型にすることでさらに下げることができます。
Aは機体の最大断面積、ρは空気密度、Uは速度です。
空気密度ρはさらに
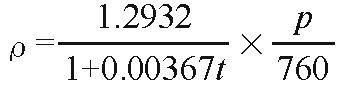
と表すことができます。
ここで、tは気温、pは圧力(mmHg)となります。
マクロモデル、ミクロモデルで示したチューブに関するスペックはこれらの式を用いて算出しています。
○排気装置.
計算の結果、マクロモデル、ミクロモデルで示しているように要求されるチューブ内の気圧はせいぜい0.1Pa程度であり、これなら現行のポンプで十分に真空引きができます。問題は真空引きしなければならない容積ですが、マクロモデルでは約東京ドーム10杯分、ミクロモデルでは1杯にも満たない体積です。これなら何とかなるかな。計算に使用したポンプの排気能力は、実際に市販されているもののデータを使用しました。ちなみに、ロータリーポンプなので、0.1Paどころか、0.00001Pa程度まで引けてしまいます。
というわけでチューブさえ設置することができれば、超高速リニアモーターカーは実現することができます。
○無重力状態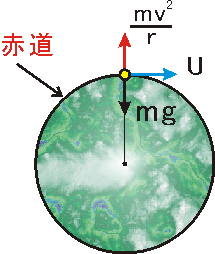
マクロモデルにおいては、無重力を得るため超高速が必要となります。ここで、回転の遠心力と地球の重力が釣り合う条件を導いてみます。
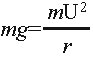
左辺が重力、右辺が遠心力であり、
m:機体の質量
g:重力加速度(9.81m/s/s)
U:機体の速度
r:回転半径(赤道半径)
となります。
これより、28800km/hで遠心力と重力が均衡し、無重力状態を得ることができます。また、赤道4万kmのチューブの敷設が困難な場合、緯度を上げて回転半径を小さくすることが考えられ、速度を上げることで遠心力と重力を平衡させることができます。ただし、地面と水平方向の遠心力成分が発生するため、横方向から磁気をかけ軌道を固定しなければなりません。
|